Integrales de Línea
Para las integrales de línea vamos a definir un vector posición r (u) el cual va a ser igual a r(u) = x (u) i + y (u) j + z (u) k para puntos cualquiera dado P (x, y, z) y este vector posición define una curva que una los puntos P1 y P2. Ahora, vamos a suponer que la curva C estará compuesta de un número finito de curvas en donde para cada una de estas curvas, nuestro vector posición r(u) va tener una derivada.
A continuación vamos a necesitar una función vectorial de posición definida y continuar a lo largo de la curva C y esta función será A (x, y z) = A1i + A2j + A3k de tal manera que vamos a definir la integral de línea de A a lo largo de la curva C entre dos puntos P1 y P2. De tal manera que vamos a obtener el producto punto de la función A y el vector posición r(u) para obtener la primer integral de la imagen. (Recuerda que obtendremos un escalar)
También será común encontrarnos con ejercicios donde tengamos una curva cerrada, es decir, una curva que no se interseca consigo misma en ningún punto, para esos casos denotaremos la integral como la segunda integral de la imagen, siendo la integral cerrada del productor punto de la función A y el vector posición r(u) obteniendo un escalar.
Formulario: http://j.gs/Emus
Teoría y Ejercicios:
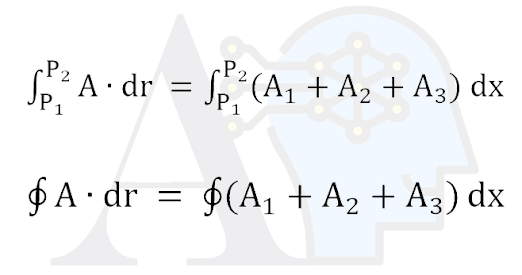




No hay comentarios.:
Publicar un comentario