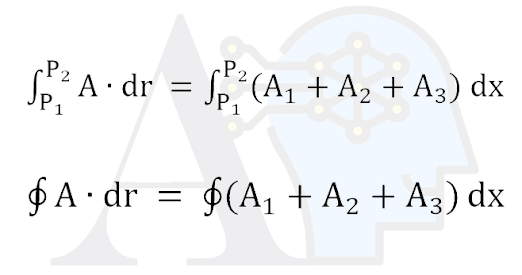Teorema de Divergencia de Gauss

 Teorema Divergencia de Gauss

Una vez aprendido el operador nabla y las integrales de línea, superficie y volumen vamos a observar que existe una relación entre una integral doble sobre alguna regiones de R en el plano y una integral de línea, así como existe una relación entre la integral de volumen y la integral doble de superficie.

De manera muy simple tenemos que el teorema de divergencia de Gauss el cual podemos diferenciarlo de manera muy sencilla porque esta basado en el productor punto. Como todo lo que conocemos de Gauss vamos a suponer que tenemos un volumen V el cual estará limitado por una superficie cerrada S en donde tendremos una función vectorial de posición A, como hemos definido anteriormente, la cual tiene derivadas continuas. Entonces tendremos las siguientes igualdades.

Básicamente esto nos dice que la integral de superficie de la normal de un vector A tomando en una superficie cerrada, es igual a la integral de la divergencia de A tomado sobre un volumen encerrado por la misma superficie. 

Los puntos que debemos recordar son

1. La divergencia esta denotada por el producto punto entre nabla y el vector posición en donde obtendremos un escalar. 

2. dv lo podemos escribir como dxdydz

3. Hay que definir antes los intervalos de integración

Con respecto a la integral de superficie

1. n es el vector normal a la superficie

2. El productor punto nos dará un vector

3. Para obtener la intervalos de integración no olvides dejar toda la integral en términos de una variable. 

Formulario:  http://j.gs/Emus

Vídeo de Teoría y ejemplos:

Integrales de Volumen

 Integrales de Volumen

De manera similar a las integrales de Superficie vamos a definir un dV siendo una parte del Volumen. Este dV lo podemos escribir como dx dy dz debido a que nuestro volumen va estar en las tres dimensiones. Dado que no tenemos que hacer algún productor punto o cruz solo debemos hacer la multiplicación de dxdydz con respecto al vector A que nos den. Después debemos definir los límites de las integrales con respecto a x, y z para comenzar a Integrar. 

Las integrales de Volumen las vamos a definir de la siguiente manera. 

Formulario:  http://j.gs/Emus

 

Video de Teoría con Ejemplos: 

Integrales de Superficie

 Integrales de Superficie

En este caso como bien nos indica el título vamos a necesitar una superficie y un vector normal unitario, n, a cualquier punto de la superficie. A partir de esta superficie podemos usar una pequeña parte de esta obteniendo un vector dS de magnitud dS el cual va en dirección n entonces como bien sabemos podemos denotarlo como dS = n dS. Entonces la Integral de Superficie la podemos definir de la siguiente manera: 

Finalmente, podemos observar que al realizar este producto punto nos lleva a obtener un escalar. 

Formulario:  http://j.gs/Emus

Video de Teoría con Ejercicios: 

 

Integrales de Línea

 Integrales de Línea

Para las integrales de línea vamos a definir un vector posición r (u) el cual va a ser igual a r(u) = x (u) i + y (u) j + z (u) k para puntos cualquiera dado P (x, y, z) y este vector posición define una curva que una los puntos P1 y P2. Ahora, vamos a suponer que la curva C estará compuesta de un número finito de curvas en donde para cada una de estas curvas, nuestro vector posición r(u) va tener una derivada. 

A continuación vamos a necesitar una función vectorial de posición definida y continuar a lo largo de la curva C y esta función será A (x, y z) = A1i + A2j  + A3k de tal manera que vamos a definir la integral de línea de A a lo largo de la curva C entre dos puntos P1 y P2. De tal manera que vamos a obtener el producto punto de la función A y el vector posición r(u) para obtener la primer integral de la imagen. (Recuerda que obtendremos un escalar)

También será común encontrarnos con ejercicios donde tengamos una curva cerrada, es decir, una curva que no se interseca consigo misma en ningún punto, para esos casos denotaremos la integral como la segunda integral de la imagen, siendo la integral cerrada del productor punto de la función A y el vector posición r(u) obteniendo un escalar. 

Formulario:  http://j.gs/Emus

Teoría y Ejercicios: 

Cálculo Vectorial - Gradiente - Divergencia - Rotacional

 Gradiente

Para realizar esta operación vamos a necesitar un operador vectorial diferencial cuyo símbolo es un triángulo invertido y es llamado Operador Nabla. Lo vamos a definir de la siguiente forma: 

Podemos observar que para realizar estas operaciones vamos a necesitar de nuestros conocimientos en derivadas diferenciales. Además cada una de las derivadas va a acompaña por los vectores unitarios i, j k. 

Cuando realizamos esta operación vamos a utilizar una función phi (x, y, z) la cuál es un función escalar definida y diferenciales en cada punto , esta operación se define de la siguiente manera: 

Básicamente esta operación consiste en hacer las derivadas parciales con respecto de x, y, z, y colocarlas en la posición de su vector unitario i, j ,k. Podemos observar que esta operación nos dará como resultado un vector y estaremos definiendo un campo vectorial. 

Divergencia. 

La divergencia es la segunda operación que podemos hacer con este operador. Para poder hacer esta operación necesitamos un vector A el cual esta definido y es diferenciable en cada punto (x, y, z)  en una región del espacio. Esta operación la vamos definir como el producto punto del operador nabla y el vector A. 

Podemos observar que utilizando las propiedades del producto punto obtendremos un escalar, como se puede ver en la imagen. Únicamente tendremos que realizar las derivas parciales de A1, A2 y A3 con respecto a x, y, z para obtener la divergencia de un vector. 

Rotacional

En el caso del rotacional tenemos que recordar como sacar determinantes de 3x3 . Como vimos anteriormente en la divergencia necesitamos un campo vectorial diferenciable el cual definimos como nuestro vector A (x, y, z) entonces el rotacional vamos a definirlo como el producto cruz entre el gradiente  y el vector A:

Podemos observar que esta operación la podemos realizar por medio de la obtención del determinante de una matriz de 3x3. De manera resumida, puedes hacer las parciales de las posiciones A1, A2 y A3 con respecto de x, y, z hacer las operaciones pertinentes y colocarlas junto a su vector unitario i, j o k. Finalmente, podemos concluir que esta operación nos va a dar otro vector. 

A continuación te dejo un link en donde puedes descargar un formulario que te ayudara a hacer tus ejercicios. También puedes encontrar un link hacia nuestro canal de YT en donde explicamos estas operación y tenemos diferentes ejercicios. 

Formulario:  http://j.gs/Emus 

Youtube: 

Integrales de Cauchy Rieman

 Integrales de Cauchy

La Fórmula de la Integral de Cauchy es bastante práctica ya que nos dice que si tenemos una función z la cual es analítica dentro y en la curva y además a es un punto interior en c entonces podemos aplicar la integral a la función de z directamente.  En la imagen podemos observar una segunda ecuación, esta será la ecuación que vamos a utilizar para obtener la derivada enésima de la función de z cuando z = a. 

Como todo concepto de la integral es más sencillo cuando lo aplicamos, a continuación te dejo unos links de ejercicios resueltos aplicando la formula de la integral de Cauchy.  Ejercicio 1 y Teoría

Estas formulas son de gran utilidad ya que muestra que si la función se conoce en la curva cerrada entonces también se pueden calcular diversas derivas en el punto c. 

Funciones Analíticas y Armónicas

 Funciones Analíticas y Armónicas

Básicamente una función es analítica si existe la derivada en todos los puntos Z de una región R. Para poder confirmar si una función es analítica o no, se utilizarán las ecuaciones de Chauchy - Rieman mostradas en la imagen como Funciones Analíticas en donde a partir de la transformación vista anteriormente, tenemos que obtener las derivadas parciales con respecto a x de la función u y esta tiene que ser igual a la derivada parcial de la función v con respecto a y. A continuación, debemos sacar la derivada parcial de la función u con respecto a y y esta tiene que ser igual a la derivada parcial de v con respecto a x. De tal manera que sí ambas derivas son iguales podemos asegurar que nuestra función será analítica. A continuación te dejo un video en donde puedes ver estas funciones aplicadas a un ejercicio. VIDEO 

En el caso de las funciones armónicas nos dicen que si la suma de la segundas derivadas de u y v con respecto a x y y existen y son continuas en una región R entonces la parte real e imaginaria de la función satisfacen las ecuaciones de laPlace siendo funciones armónicas.  VIDEO 

Transformaciones

 + Transformaciones 

Las transformaciones son otra manera en la que podemos trabajar los números complejos. La idea con la que vamos a trabajar nos dice que para cada punto que existe en el plano z existe ese punto en el plano w para entenderlo con más detalle vamos a enfocarnos en el ejercicio de abajo. 

En primer lugar tenemos que entender que la función de w estará dada por las variables u y v la cual vamos a escribir como w = u + iv siendo u la parte real y v la parte imaginaria. Entonces comenzando con una función de z siendo z elevado al cuadrado con los puntos (1, 2) comenzamos desarrollando el binomio cuadrado obteniendo z elevado al cuadrado es igual a x elevado al cuadrado + 2ixy menos y elevado al cuadrado. 

Ahora es cuando entra a detalle la transformación, en donde vamos a tomar la parte real (u)  siendo x elevado al cuadrado menos y elevado al cuadrado y la parte imaginaria (v) siendo 2xy. Finalmente, tenemos que sustituir los puntos (1, 2) con el fin de observar que el plano w existen un punto ubicado en (-3 , 4) que es una transformación de la función compleja original del punto (1,2) como se observa en la imagen. 

Acá te dejo un video de nuestro canal de Yt en donde puedes observar paso a paso como realizar este procedimiento y en donde puedes encontrar videos de ejercicios resueltos. VIDEO

Modulo, Forma Polar y Formula de Euler

 + Módulo 

El módulo de los números complejos nos ayuda a entender la expresión dada en el problema. De hecho, es bastante útil para determinar la zona y el plano z en la que estamos trabajando.  En nuestro canal de YT pueden encontrar algunos videos de ejercicios resueltos utilizando el módulo Ejercicio 1 y Ejercicio 2  . Sin embargo, esta expresión se define como el valor absoluto de z , la cual podemos escribir como la raíz cuadrada de las partes reales de la función compleja siendo x y y elevados al cuadrado como se observa en la imagen. 

+ Forma Polar

Utilizando nuestros conocimientos pasados en coordenadas polares podemos observar que al trazar un circulo de radio R, podemos definir tanto las variables x como y entorno a ese circulo de tal manera x = r cos teta y y = r sen teta, como se muestra en la imagen. Una vez definidas estas variables podemos proceder a sustituir en nuestra función compleja obteniendo z = r (cos teta + i sen teta) siendo esta la función compleja expresa en su forma polar 

+ Formula de Euler 

Euler siendo un avanzado matemático logró introducir el uso de las funciones exponenciales con las funciones trigonométricas. De ahí que en la parte inferior de la imagen se puede observar de manera resumida su formula siendo bastante útil al momento de utilizar complejos. En términos sencillos nos dice que si tenemos una función exponencial compleja es decir, e elevado a la iteta esta función la podemos expresar en funciones trigonométricas como se muestra en la imagen. 

Operaciones Fundamentales de los Números Complejos

 Operaciones Fundamentales 

+ Suma y Resta

Como se puede observar en la imagen, la suma de dos números complejos comienza por la suma de las partes reales siendo ( a + c ). A continuación se realiza la suma de la parte real de la parte imaginaria siendo (b + d). Finalmente, colocamos la parte imaginaria de la suma i(b + d) obteniendo como resultado (a + c) + i (b + d).

Al realizar la resta de dos números complejos se siguen los mimos pasos. En primer lugar, se realiza la resta de las partes reales (a - c). A continuación, se realiza la resta de la parte real de la parte imaginaria (b - d). Finalmente, colocamos la parte imaginaria de la resta i(b -d) obteniendo como resultado (a- c) + i(b - d). Como se muestra en la siguiente imagen. 

+ Multiplicación 

Para realizar la multiplicación de dos números complejos se utiliza el álgebra aprendida en la multiplicación de dos polinomios, es decir, en primer lugar a multiplicara todo el segundo número complejo, después la parte imaginaria ib multiplicara el segundo número complejo para que al final separemos la parte real y la parte imaginaria con el fin de volverlo a escribir es su forma z = x + ib como se muestra en la imagen. 

NOTA: Recuerda que al momento de multiplica (ib)(id) = -bd debido que al multiplicar i por i obtendremos -1. 

+ División

El caso de la división no es como la división en los números reales. Esta vez se emplea el complejo conjugado del denominador, el cuál es multiplicado por toda la fracción original con el fin de poder obtener las partes reales e imaginarias de la fracción. 

¿Qué son los números complejos?

 

Números Complejos 

Los números complejos son denotados usualmente con una letra z y estos tienen la forma a + ib donde a usualmente se sustituye con x y b con y. Estos números se caracterizan por tener una parte real e imaginaria, en donde a es la parte real mientras que b es la parte imaginaria. En dado caso que a = 0 tendríamos z = ib siendo esta la representación de un número imaginario puro. 

Dentro de los números complejos existe el complejo conjugado denotado con un superíndice en la z (como se muestra en la imagen) básicamente este número consta en poner un signo negativo en la parte imaginaria del complejo. El complejo conjugado es bastante usado al momento de racionalizar una fracción y de igual manera se puede utilizar al momento de normalizar una función. 

La parte imaginaria nace de la raíz de un número negativo, enfocándonos específicamente al número menos uno. Siendo esta denominada la parte imaginaria. Hay varias operaciones que destacan entre los imaginarios siendo la multiplicación la más importante. Como se observa en la imagen, al multiplicar i por i obtendríamos una i elevada al cuadrado que al sustituir por la raíz de -1 obtendríamos que i elevado al cuadrado es igual a -1. Siendo esta una operación fundamental dado que es muy usada y confusa dentro de los números complejos. 

Números Complejos

Números Complejos 

Los números complejos son denotados usualmente con una letra z y estos tienen la forma a + ib donde a usualmente se sustituye con x y b con y. Estos números se caracterizan por tener una parte real e imaginaria, en donde a es la parte real mientras que b es la parte imaginaria. En dado caso que a = 0 tendríamos z = ib siendo esta la representación de un número imaginario puro. 

Dentro de los números complejos existe el complejo conjugado denotado con un superíndice en la z (como se muestra en la imagen) básicamente este número consta en poner un signo negativo en la parte imaginaria del complejo. El complejo conjugado es bastante usado al momento de racionalizar una fracción y de igual manera se puede utilizar al momento de normalizar una función. 

La parte imaginaria nace de la raíz de un número negativo, enfocándonos específicamente al número menos uno. Siendo esta denominada la parte imaginaria. Hay varias operaciones que destacan entre los imaginarios siendo la multiplicación la más importante. Como se observa en la imagen, al multiplicar i por i obtendríamos una i elevada al cuadrado que al sustituir por la raíz de -1 obtendríamos que i elevado al cuadrado es igual a -1. Siendo esta una operación fundamental dado que es muy usada y confusa dentro de los números complejos. 

Operaciones Fundamentales 

+ Suma y Resta

Como se puede observar en la imagen, la suma de dos números complejos comienza por la suma de las partes reales siendo ( a + c ). A continuación se realiza la suma de la parte real de la parte imaginaria siendo (b + d). Finalmente, colocamos la parte imaginaria de la suma i(b + d) obteniendo como resultado (a + c) + i (b + d).

Al realizar la resta de dos números complejos se siguen los mimos pasos. En primer lugar, se realiza la resta de las partes reales (a - c). A continuación, se realiza la resta de la parte real de la parte imaginaria (b - d). Finalmente, colocamos la parte imaginaria de la resta i(b -d) obteniendo como resultado (a- c) + i(b - d). Como se muestra en la siguiente imagen. 

+ Multiplicación 

Para realizar la multiplicación de dos números complejos se utiliza el álgebra aprendida en la multiplicación de dos polinomios, es decir, en primer lugar a multiplicara todo el segundo número complejo, después la parte imaginaria ib multiplicara el segundo número complejo para que al final separemos la parte real y la parte imaginaria con el fin de volverlo a escribir es su forma z = x + ib como se muestra en la imagen. 

NOTA: Recuerda que al momento de multiplica (ib)(id) = -bd debido que al multiplicar i por i obtendremos -1. 

+ División

El caso de la división no es como la división en los números reales. Esta vez se emplea el complejo conjugado del denominador, el cuál es multiplicado por toda la fracción original con el fin de poder obtener las partes reales e imaginarias de la fracción. 

+ Módulo 

El módulo de los números complejos nos ayuda a entender la expresión dada en el problema. De hecho, es bastante útil para determinar la zona y el plano z en la que estamos trabajando.  En nuestro canal de YT pueden encontrar algunos videos de ejercicios resueltos utilizando el módulo Ejercicio 1 y Ejercicio 2  . Sin embargo, esta expresión se define como el valor absoluto de z , la cual podemos escribir como la raíz cuadrada de las partes reales de la función compleja siendo x y y elevados al cuadrado como se observa en la imagen. 

+ Forma Polar

Utilizando nuestros conocimientos pasados en coordenadas polares podemos observar que al trazar un circulo de radio R, podemos definir tanto las variables x como y entorno a ese circulo de tal manera x = r cos teta y y = r sen teta, como se muestra en la imagen. Una vez definidas estas variables podemos proceder a sustituir en nuestra función compleja obteniendo z = r (cos teta + i sen teta) siendo esta la función compleja expresa en su forma polar 

+ Formula de Euler 

Euler siendo un avanzado matemático logró introducir el uso de las funciones exponenciales con las funciones trigonométricas. De ahí que en la parte inferior de la imagen se puede observar de manera resumida su formula siendo bastante útil al momento de utilizar complejos. En términos sencillos nos dice que si tenemos una función exponencial compleja es decir, e elevado a la iteta esta función la podemos expresar en funciones trigonométricas como se muestra en la imagen. 

+ Transformaciones 

Las transformaciones son otra manera en la que podemos trabajar los números complejos. La idea con la que vamos a trabajar nos dice que para cada punto que existe en el plano z existe ese punto en el plano w para entenderlo con más detalle vamos a enfocarnos en el ejercicio de abajo. 

En primer lugar tenemos que entender que la función de w estará dada por las variables u y v la cual vamos a escribir como w = u + iv siendo u la parte real y v la parte imaginaria. Entonces comenzando con una función de z siendo z elevado al cuadrado con los puntos (1, 2) comenzamos desarrollando el binomio cuadrado obteniendo z elevado al cuadrado es igual a x elevado al cuadrado + 2ixy menos y elevado al cuadrado. 

Ahora es cuando entra a detalle la transformación, en donde vamos a tomar la parte real (u)  siendo x elevado al cuadrado menos y elevado al cuadrado y la parte imaginaria (v) siendo 2xy. Finalmente, tenemos que sustituir los puntos (1, 2) con el fin de observar que el plano w existen un punto ubicado en (-3 , 4) que es una transformación de la función compleja original del punto (1,2) como se observa en la imagen. 

Acá te dejo un video de nuestro canal de Yt en donde puedes observar paso a paso como realizar este procedimiento y en donde puedes encontrar videos de ejercicios resueltos. VIDEO

+ Funciones Analíticas y Armónicas

Básicamente una función es analítica si existe la derivada en todos los puntos Z de una región R. Para poder confirmar si una función es analítica o no, se utilizarán las ecuaciones de Chauchy - Rieman mostradas en la imagen como Funciones Analíticas en donde a partir de la transformación vista anteriormente, tenemos que obtener las derivadas parciales con respecto a x de la función u y esta tiene que ser igual a la derivada parcial de la función v con respecto a y. A continuación, debemos sacar la derivada parcial de la función u con respecto a y y esta tiene que ser igual a la derivada parcial de v con respecto a x. De tal manera que sí ambas derivas son iguales podemos asegurar que nuestra función será analítica. A continuación te dejo un video en donde puedes ver estas funciones aplicadas a un ejercicio. VIDEO 

En el caso de las funciones armónicas nos dicen que si la suma de la segundas derivadas de u y v con respecto a x y y existen y son continuas en una región R entonces la parte real e imaginaria de la función satisfacen las ecuaciones de laPlace siendo funciones armónicas.  VIDEO 

+ Integrales de Cauchy

La Fórmula de la Integral de Cauchy es bastante práctica ya que nos dice que si tenemos una función z la cual es analítica dentro y en la curva y además a es un punto interior en c entonces podemos aplicar la integral a la función de z directamente.  En la imagen podemos observar una segunda ecuación, esta será la ecuación que vamos a utilizar para obtener la derivada enésima de la función de z cuando z = a. 

Como todo concepto de la integral es más sencillo cuando lo aplicamos de tal manera que a continuación te dejos unos link de ejercicios resueltos con aplicando la formula de la integral de Cauchy.  Ejercicio 1 y Teoría

Estas formulas son de gran utilidad ya que muestra que si la función se conoce en la curva cerrada entonces también se pueden calcular diversas derivas en el punto c. 

Matriz Triangulo Superior e Inferior

 Matriz Triangulo Superior e Inferior 

Las matrices de triángulo superior e inferior son muy utilizadas como alternativa para sacar determinantes de matrices mayores de 3x3 debido a que se pueden realizar operaciones sencillas con el fin de dejar una matriz A expresada como una matriz triangulo superior o inferior, en donde su determinante será la multiplicación de todos los elementos ubicados en la diagonal principal. 

De manera muy sencilla, la matriz triangulo superior es aquella en donde sus elementos debajo de la diagonal principal son ceros, mientras que dentro de la matriz de triángulo inferior se observa que todos los elementos por encima de la diagonal principal son cero. 

A continuación vamos a ver ejemplificado ambos casos: 

+ Como sacar Determinantes 4x4 o más, utilizando la matriz triángulo superior

Partiendo de una matriz A cualquiera lo primero que haremos es hacer cero todos los elementos debajo del primer elemento de la diagonal principal, en este caso sería el elemento a11. ¿Como haremos esto? Bueno en la imagen pueden observar que tenemos marcados en rojo ciertas operaciones. En este caso se utiliza una fila pivote , es decir, utilizamos una fila la cual vamos a multiplicar por n número y después vamos a sumar o resta toda esa fila a otra con el fin de hacer cero un elemento.

Vamos más despacio. En este caso nuestro fila pivote es la primera fila, con lo elementos 1 5 2 4. De acuerdo a la primera operación marcada en rojo, esta primera fila la vamos a multiplicar por -3 de tal manera que nuestra fila ahora esta conformada por los elementos - 3-15 -6 -12. A continuación, estos elementos serán sumados a la fila 3 de tal manera que realizaremos esta operación en la fila 3 obteniendo los siguientes elementos (-3+3) (-15+0) (-6+1) (-12+1) = 0 -15 -5 -11 mostrados en la segunda parte de la figura. A continuación, realizaremos la operación 2) de la misma forma. 

Podemos observar que en nuestra matriz resultante, ahora tenemos en ceros todos los elementos debajo de la diagonal superior. Ahora vamos a cambiar nuestra fila pivote por la segunda fila de la matriz resultante, debido a que en la segunda fila ya contamos con un cero en la posición a21 esto nos dice que al realizar cualquier operación NO modificará los ceros que anteriormente hemos realizado. Finalmente, se realizan las operación descritas en los incisos 3) y 4) con el fin de hacer ceros todos los elementos debajo del segundo elemento de la diagonal principal. 

Obteniendo nuestra matriz resultante es evidente ver que falta hacer cero el último elemento ubicado debajo del tercer elemento de la diagonal principal. Para hacer este elemento cero, vamos a utilizar la tercera fila como nuestra fila pivote debido que al multiplicarla por cualquier número no afectara los ceros que previamente hemos realizado. Finalmente, al realizar la operación del inciso 5); obtenemos la matriz triangulo superior y no nos queda más que realizar la multiplicación de cada uno de los elementos de la diagonal principal para así obtener el determinante de la matriz.

+ Como sacar Determinantes 4x4 utilizando la matriz triángulo inferior

Sacar el determinante de una matriz a partir de una matriz triángulo inferior es similar al procedimiento de la matriz triángulo superior.  En este caso vamos a comenzar haciendo ceros todos los elementos arriba del ultimo elemento de la diagonal principal utilizando la ultima fila de la matriz original como nuestra fila pivote y realizando la operaciones 1), 2) y 3). 

Una vez realizadas estas operaciones obtenemos la matriz resultante del lado superior derecho de la imagen mostrando los ceros arriba del ultimo elemento de la diagonal principal. A continuación, utilizaremos la fila 2 como la fila pivote con el fin de no dañar los ceros que hemos realizados. Al realizar las operaciones 4) y 5) mostradas en la parte de abajo de la matriz resultante lograremos hacer cero los elementos superiores al 3er elemento de la diagonal principal. 

Ahora, podemos ver en la imagen en la parte derecha inferior la matriz resultante de estas operaciones. Es evidente ver que estamos a punto de conseguir la matriz triángulo inferior únicamente nos hace falta hacer cero el elemento superior al segundo elemento de la diagonal principal, procedimiento que podemos lograr a partir de la última operación marcada en la parte baje de esa matriz. 

Finalmente, obtenemos la matriz triángulo inferior, en donde vamos a extraer los elementos ubicados en la diagonal principal y vamos a multiplicarlos con el fin de obtener el determinante de la matriz A (original). 

En caso de que tengas mas dudas de como utilizar la matriz triangulo superior les dejo este vídeo de nuestro canal de Youtube: Matriz Triangulo Superior e Inferior

Ejercicios Recomendados (Canal YT)

Operaciones Fundamentales 

Formulario Matrices - DESCARGAR 

Bibliografía Recomendada

Álgebra Lineal - Stanley I. Grossman - 7ma edición

Analisis Vectorial - Schaum - 2da Edición

Advanced Mathematics for Engineers and Scientist - Schaum

Determinante 3x3

 Determinantes 3x3 

Vamos a entender como sacar determinantes de 3x3. Vamos a basarnos en los determinantes de 2x2. En primer lugar vamos a tomar la fila 1 y la columna 1, podemos observar que al quitar esta fila y columna obtenemos una matriz de 2x2 como vemos en el inciso 1). A continuación vamos a tomar el elemento que esta dentro de la unión de la fila 1 y columna 1 en este caso es el 9. Finalmente, el 9 va a multiplicar el determinante de la matriz 2x2 resultante. (Este seria nuestro primer paso)

A continuación, vamos a tomar la primera fila y la segunda columna. Realizaremos el mismo procedimiento en donde podemos observar que ahora el elemento que esta encerrado por la unión de la primera fila y la segunda columna es 1, sin embargo, la suma de la primera fila y segunda columna nos va a dar un número impar, por ende, en todas las sumas impares vamos a colocar un signo negativo en elemento encerrado es por esto que el determinante de la matriz 2x2 será multiplicado por -1.

Ahora, se toma la primera fila y tercera columna, al ser su suma par no se agrega un negativo y podemos observar que el elemento resultante de la unión de la fila y columna seleccionada es 4. Este elemento se multiplica por el determinante de la matriz resultante. 

Finalmente, se realiza las sumas y restas necesarias de todos los resultados obtenidos, siendo el resultado final el determinante de la matriz 3x3.

Formulario Matrices - DESCARGAR 

Bibliografía Recomendada

Álgebra Lineal - Stanley I. Grossman - 7ma edición

Analisis Vectorial - Schaum - 2da Edición

Advanced Mathematics for Engineers and Scientist - Schaum

Menor y Cofactor

 Menor y Cofactor

MENOR

El menor es uno de los temas más sencillos, sin embargo, importantes ya que nos ayudarán a obtener los cofactores de una matriz. De manera sencilla, obtenemos el Menor mxn al remover las filas y columnas que nos menciona el menor y este se denota con los elementos restantes de la matriz. Vamos a ejemplificarlo, en el caso mostrado en la imagen en donde nos piden el Menor 22 removemos la fila y columna dos, de tal manera que los elementos restantes pasaran a ser parte de nuestra nueva matriz. Como segundo ejemplo, nos piden el Menor 13 de tal manera que esta vez removemos la fila 1 y la columna 3, observando que los elementos  restantes de la matriz formarán parte de nuestra nueva matriz. 

COFACTOR

Una vez definido el concepto del menor vamos a introducirnos al concepto de COFACTOR ya que este es primordial para obtener la matriz inversa la cual utilizamos con gran regularidad para darle solución a diferentes sistemas de ecuaciones. 

A partir de una matriz A obtenemos el cofactor denotado como A nxm; utilizando la fórmula mostrada en la imagen podemos observar que si la suma de n+m es par nuestro cofactor será positivo, por otra parte, si es impar nuestro cofactor será negativo. A continuación, se observa que se obtendrá el determinante del menor, que en el caso del ejercicio resulta ser una matriz sencilla de 2x2, sin embargo, podemos tener ejercicios donde el determinante sea de 3x3, 4x4... etc. 

Formulario Matrices - DESCARGAR 

Bibliografía Recomendada

Álgebra Lineal - Stanley I. Grossman - 7ma edición

Analisis Vectorial - Schaum - 2da Edición

Advanced Mathematics for Engineers and Scientist - Schaum

Determinantes 2x2

 Determinantes 2x2

Ahora aprenderemos a sacar determinantes de 2x2. Este es el caso ideal y uno de los más sencillos, básicamente lo que tenemos que hacer es multiplicar el elemento a11 por el elemento a22 y restarle la multiplicación de los elementos a12 por el elemento a21. Como se muestra en la imagen: 

Cabe recalcar que los determinantes se escriben como det A o como valor absoluto. 

Formulario Matrices - DESCARGAR 

Bibliografía Recomendada

Álgebra Lineal - Stanley I. Grossman - 7ma edición

Analisis Vectorial - Schaum - 2da Edición

Advanced Mathematics for Engineers and Scientist - Schaum

Tipos de Matrices

 Tipos de Matrices

Existen diferentes matrices de diferente orden de diferente todo, sin embargo, tenemos 5 matrices típicas de las cuales vale la pena hablar. 

En primer lugar la matriz Unitaria es aquella matriz cuadrada en la cual todos sus elementos son 1 en su diagonal principal mientras que los otros elementos son ceros. Esta matriz es muy utilizada al momento de hacer demostraciones ya que la podemos utilizar como la unidad. Cuenta con una gran propiedad en donde una matriz multiplicada por la matriz unitaria nos va a dar la misma matriz, es decir: 

AI = IA = A

La matriz Cero o Nula es bastante sencilla ya que todos los elementos dentro de esta son igual a cero y es denotada por una O o un cero 0 como se ve en la imagen.

La Matriz Cuadrada es una matriz en donde el número de filas es igual al número de columnas, es decir, n = m y la podemos escribir como nxn. Esta matriz es de la más usadas debido a que se cumplen todas las condiciones para poder hacer las operaciones básicas como lo son las sumas, restas o multiplicaciones. 

Finalmente, la Matriz Fila y Columna son matrices básicas, en donde, claramente la matriz fila consta de elementos acomodados en una única fila. Ahora, la matriz Columna son elementos acomodados en una única columna. Estas dos matrices son utilizadas de manera común para realizar las operaciones de multiplicación. 

Formulario Matrices - DESCARGAR 

Bibliografía Recomendada

Álgebra Lineal - Stanley I. Grossman - 7ma edición

Analisis Vectorial - Schaum - 2da Edición

Advanced Mathematics for Engineers and Scientist - Schaum

Diagonal Principal y Traza

 Diagonal Principal y Traza

La Diagonal Principal es uno de los conceptos más importantes dentro del mundo de las matrices ya que la utilizaremos para obtener el determinante de matrices de más de 3x3. Bueno, en términos sencillos la diagonal principal no es más que todos los elementos en donde el número de filas es igual al número de columnas, es decir, todos los elementos a11, a22, a33 ..... anm donde n=m como lo vemos ejemplificado en la imagen. 

Ahora la traza se construye a partir de la suma de todos aquellos elementos encontrados dentro de la diagonal principal. 

Formulario Matrices - DESCARGAR 

Bibliografía Recomendada

Álgebra Lineal - Stanley I. Grossman - 7ma edición

Analisis Vectorial - Schaum - 2da Edición

Advanced Mathematics for Engineers and Scientist - Schaum

Matriz Transpuesta

 Matriz Transpuesta 

La matriz transpuesta es una operación necesaria dentro del mundo de matrices debido a que es utilizada para obtener la matriz inversa. Además, esta matriz nos ayuda a realizar diversas demostraciones. La operación de esta matriz consta en tomar la primera fila de la matriz y colocarla como la primera columna. A continuación, se toma la segunda fila y se coloca como la segunda columna. Esta operación se realiza de acuerdo el número de filas que tenga la matriz. Cabe recalcar que la matriz transpuesta es denotada con la letra original que define a la matriz sólo que se le agrega un T como superíndice como se muestra en la siguiente imagen: 

A continuación les dejo un vídeo en nuestro canal de Youtube explicando estos temas y otros como lo son la Matriz Skew y la matriz simétrica. Ver vídeo

Formulario Matrices - DESCARGAR 

Bibliografía Recomendada

Álgebra Lineal - Stanley I. Grossman - 7ma edición

Analisis Vectorial - Schaum - 2da Edición

Advanced Mathematics for Engineers and Scientist - Schaum